Chapitre 1 : Translation et Vecteur
Chapitre 2 : Coordonnées et Vecteur
1- Translation et vecteur
1A. Définitions
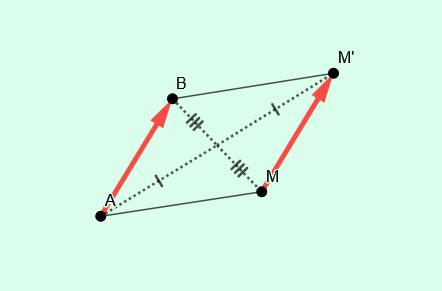
- Soit \(A\) et \(B\) deux points donnés. On appelle image d’un point \(M\) par la translation qui transforme \(A\) en \(B\) le point \(M’\) tel que \([AM’]\) et \([BM]\) ont le même milieu, c’est-à-dire tel que \(ABM’M\) est un parallélogramme.
- A la translation qui transforme \(A\) en \(B\), on associe le vecteur \(\overrightarrow{AB}\) qui symbolise le déplacement de \(A\) vers \(B\) ou de \(M\) vers \(M’\).
On le représente par une flèche allant de \(A\) jusqu’à \(B\).
1B. Égalité de vecteurs
Soit \(M’\) l’image d’un point \(M\) par la translation associée à un vecteur \(\overrightarrow{AB}\).
Les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{MM’}\) sont dits égaux. On note \(\overrightarrow{AB}=\overrightarrow{MM’}\).
Soit \(A\),\(B\),\(C\) et \(D\) quatre points distincts. On a :
\(\overrightarrow{AB}=\overrightarrow{CD}\Longleftrightarrow D\) est l’image de \(C\) par la translation associée au vecteur \(\overrightarrow{AB}\) ;
\(\quad\qquad\qquad\Longleftrightarrow [AD]\) et \([BC]\) ont le même milieu ;
\(\quad\qquad\qquad\Longleftrightarrow ABDC\) est un parallélogramme.
1C. Somme de deux vecteurs
Soit \(A\),\(B\) et \(C\) trois points.
Appliquer la translation associée au vecteur \(\overrightarrow{AB}\), puis la translation associée au vecteur \(\overrightarrow{BC}\), revient à appliquer la translation associée au vecteur \(\overrightarrow{AC}\).
Le vecteur \(\overrightarrow{AC}\) est appelé vecteur somme des vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{BC}\).
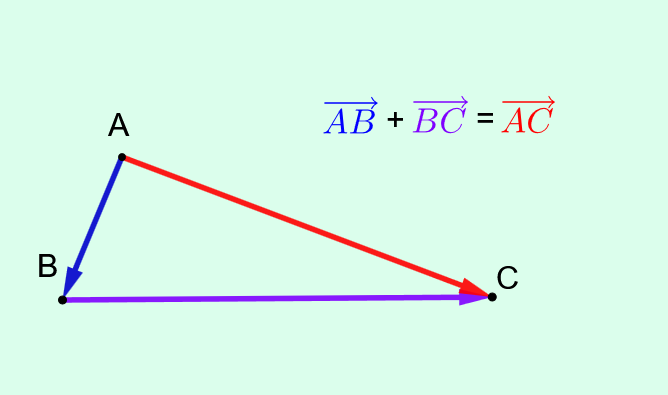
Relation de Chasles
Soit \(A\),\(B\) et \(C\) trois points. On a :
\(\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}\).
Remarque :
Soit \(A\) et \(B\) deux points. D’après la relation de Chasles, on a \(\overrightarrow{AB} + \overrightarrow{BA} = \overrightarrow{AA}\).
Le vecteur \(\overrightarrow{AA}\) est dit vecteur nul. On le note \(\overrightarrow{0}\) et on a \(\overrightarrow{BA}=\overrightarrow{-AB}\).
2- Coordonnées et vecteur
2A. Coordonnés d’un vecteur
- Définition
Soit \(M(x;y)\) un point dans un plan muni d’un repère d’origine \(O\).
Soit \(\overrightarrow{u}\) un vecteur égal à \(\overrightarrow{OM}\).
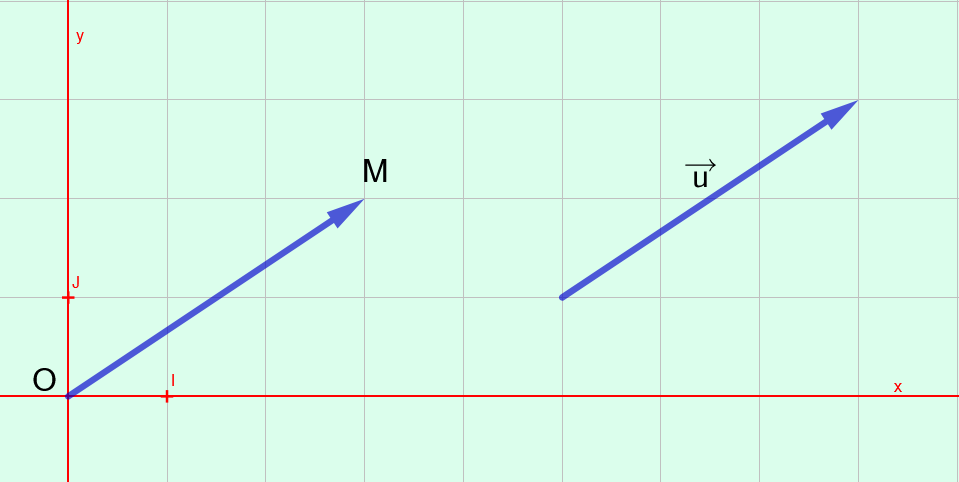
Les coordonnées de \(\overrightarrow{u}\) sont \(\begin{pmatrix} x \\ y \\\end{pmatrix}\)
.
- Egalité de deux vecteurs
Deux vecteurs \(\overrightarrow{u} \begin{pmatrix} x \\ y \\\end{pmatrix}\) et \(\overrightarrow{v}\begin{pmatrix} x’ \\ y’ \\\end{pmatrix}\) sont égaux si et seulement s’ils ont les mêmes coordonnées.
Soit \(A( x_A ; y_A )\) et \(B( x_B ; y_B )\) deux points du plan muni d’un repère.
On a : \(\overrightarrow{AB} \begin{pmatrix} x_B-x_A \\ y_B-y_A \\\end{pmatrix}\)
Remarque :
Pour montrer qu’un quadrilatère \(ABCD\) est un pârallélogramme, il suffit de montrer à l’aide des coordonnées que deux vecteurs tels que \(\overrightarrow{AB}\) et \(\overrightarrow{DC}\) sont égaux.
2B. Opérations sur les coordonnées
- Somme de deux vecteurs
Soit deux vecteurs \(\overrightarrow{u} \begin{pmatrix} x \\ y \\\end{pmatrix}\) et \(\overrightarrow{v}\begin{pmatrix} x’ \\ y’ \\\end{pmatrix}\).
Le vecteur somme \(\overrightarrow{u} +\overrightarrow{v}\) a pour coordonnées \(\begin{pmatrix} x + x’ \\ y + y’ \\\end{pmatrix}\).
- Produit d’un vecteur par un réel
Soit \(k\) un réel et \(\overrightarrow{u} \begin{pmatrix} x \\ y \\\end{pmatrix}\) un vecteur.
Le produit du vecteur \(\overrightarrow{u}\) par le réel \(k\) est le vecteur noté \(k \overrightarrow{u}\) et de coordonnées \(\begin{pmatrix} kx \\ ky \\\end{pmatrix}\)
- Norme d’un vecteur.
Soit \(\overrightarrow{u} \begin{pmatrix} a \\ b \\\end{pmatrix}\) un vecteur dans le plan muni d’un repère orthonormé.
On appelle norme de \(\overrightarrow{u}\) le nombre noté avec : \(|| \vec u ||\)
\(|| \vec u ||=\sqrt{a^2+b^2}\)
3- Colinéarité
3A. Définition
Soit \(\overrightarrow{u}\) et \(\overrightarrow{v}\) deux vecteurs non nuls.
Ces vecteurs sont colinéaires, si et seulement si, il existe un réel \(k\) tel que \(\overrightarrow{v}=k \overrightarrow{u}\).
Remarque :
Si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont deux vecteurs non nuls avec \(\overrightarrow{v}=k \overrightarrow{u}\), alors \(\overrightarrow{u}=\frac{1}{k}\overrightarrow{v}\).
Le vecteur nul est colinéaire à tout vecteur \(\overrightarrow{u}\), car on a \(\overrightarrow{0}=0 \overrightarrow{u}\).
3B. Propriété
Soit \(\overrightarrow{u} \begin{pmatrix} x \\ y \\\end{pmatrix}\) et \(\overrightarrow{v}\begin{pmatrix} x’ \\ y’ \\\end{pmatrix}\) deux vecteurs.
Ces vecteurs sont colinéraires, si et seulement si, leur déterminant \(xy’-x’y\) est nul.
3C. Application de la colinéarité
- Points alignés
Soit \(A\),\(B\) et \(C\) trois points deux à deux distincts.
Les points \(A\),\(B\) et \(C\) sont alignés, si et seulement si, \(\overrightarrow{AB}\) et \(\overrightarrow{AC}\) sont colinéaires.
- Droites parallèles
Soit \(A\),\(B\),\(C\) et \(D\) quatre points deux à deux distincts.
Les droites \((AB)\) et \((CD)\) sont parallèles, si et seulement si, \(\overrightarrow{AB}\) et \(\overrightarrow{DC}\)sont colinéaires.