Chapitre 1 : Moyenne – Etendue
Chapitre 2 : Médiane – Écart interquartile
1- Moyenne – Étendue
1A. Moyenne
Soit \(x_1,x_2,x_3,…,x_n\) une série statistique quantitative de \(n\) valeurs.
La moyenne arithmétique simple de la série, notée \(\bar{x}\), est le quotient de la somme des valeurs par l’effectif total \(n\) :
\(\bar{x}= \frac{x_1+x_2+x_3+…+x_n}{n}\)
Soit \(x_1,x_2,x_3,…,x_n\) une série statistique quantitative de \(n\) valeurs affectée de coefficients respectifs \(e_1,e_2,e_3,…e_n\).
La moyenne pondérée de la série, noté \(\bar{x}\), est le quotient de la somme des produits de chaque valeur par son coefficient respectif par la somme des coefficients :
\(\bar{x}= \frac{e_1 x_1+e_2 x_2+e_3 x_3+…+e_n x_n}{e_1 + e_2 + e_3 + … + e_n}\)
Exemple : Les notes d’un élève sont 6 ; 12 ; 7 ; 14 ; 10
Sa moyenne arithmétique est : \(\bar{x}= \frac{6+12+7+14+10}{5}=\frac{49}{5}\), soit 9.8.
Affectée des coefficients respectifs 2 ; 5 ; 3 ; 6 ; 4, la moyenne pondérée de ses notes est :
\(\bar{x}= \frac{2\times6+5\times12+3\times7+6\times14+4\times10}{2+5+3+6+4}=\frac{217}{20}\) soit 10,85.
2B. Écart type
Soit \(x_1,x_2,x_3,…,x_n\) une série statistique quantitative de \(n\) valeurs de moyenne \(\bar{x}\)
L’écart type de la série est la racine carrée de la moyenne des carrés des différences entre les \(x_i\) et la moyenne. On le note \(\sigma\).
\(\sigma = \sqrt{ \frac {(x_1 -\bar{x})^2 + (x_2 -\bar{x})^2 + … + (x_n -\bar{x})^2}{n}}\)
Exemple : Les notes d’un élève sont 6 ; 12 ; 7 ; 14 ; 10 de moyenne 9,8.
L’écart type est \(\sigma = \sqrt{ \frac {(6-9,8)^2 + (12-9,8)^2 + … + (10-9,8)^2}{5}}\), soit environ 2,99
La moyenne est une caractéristique de position, souvent complétée par une caractéristique de dispersion ( qui peut être l’écart type ).
2- Médiane – Écart interquartile
2A. Effectifs – Fréquences
Dans une série statistique, on appelle effectif cumulé croissant d’une valeur, la somme de l’effectif de cette valeur et des effectifs des valeurs plus petites.
Dans une série statistique, la fréquence d’une valeur est l’effectif de cette valeur divisé par l’effectif total.
On appelle fréquence cumulée croissante d’une valeur, le quotient de son effectif cumulé croissant par l’effectif total de la série.
Exemple : On considère la série statistique suivant :
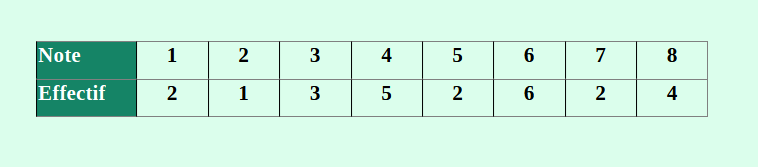
L’effectif total de la série est : \(2+1+3+5+2+6+2+4\) soit 25.
La fréquence de la note 5 est : \(\frac{2}{25}\), soit 0,08.
L’effectif cumulé croissant de la note 5 est : \(2+1+3+5+2\) soit 13.
La fréquence cumulée croissante de la note 5 est : \(\frac{13}{25}\), soit 0.52.
2B. Médiane – Quartiles
Soit \(x_1,x_2,x_3,…,x_n\) une série statistique quantitative de \(n\) valeurs.
On appelle médiane de la série, notée \(Me\), une valeur telle :
que 50% au moins des valeurs de la série soient inférieures ou égales à \(Me\) ;
et que 50% au moins des valeurs de la série soient supérieures ou égales à \(Me\)
Exemple : On considère la série ordonnée \(A\) :
2 ; 3 ; 5 ; 10 ; 11 ; 12 ; 13 ; 14 ; 16.
Il y a neuf valeurs, donc la médiane est la cinquième valeur, soit 11.
En effet, il y a cinq valeurs inférieures ou égales à 11 ( 2 ; 3 ; 5 ; 10 et 11 ).
Le pourcentage de valeurs inférieures ou égales à 11 est :
\(\frac{5}{9} \times 100% \) , soit environ 55,6%.
De même, il y a cinq valeurs supérieures ou égales à 11 ( 11 ; 12 ; 13 ; 14 et 16 ).
Le pourcentage de valeurs supérieures ou égales à 11 est :
\(\frac{5}{9} \times 100% \) , soit environ 55,6%.
On appelle premier quartile de la série, notée \(Q_1\), la plus petite valeur de la série telle :
_ que 25% au moins des valeurs de la série soient inférieures ou égales à \(Q_1\) ;
_ et que 75% au moins des valeurs de la série soient supérieures ou égales à \(Q_1\).
On appelle troisième quartile de la série, notée \(Q_3\), la plus petite valeur de la série telle :
_ que 75% au moins des valeurs de la série soient inférieures ou égales à \(Q_3\);
_et que 25% au moins des valeurs de la série soient supérieures ou égales à \(Q_3\).
2C. Ecart interquartile
Soit une série statistique de premier quartile \(Q_1\) et de troisième quartile \(Q_3\).
On appelle écart interquartile de la série, le nombre \(Q_3-Q_1\).
Remarques :
La médiane est une caractéristique de position, souvent complétée par une caractéristique de dispersion qui peut être l’écart interquartile.
Médiane et écart interquartile sont peu sensibles aux valeurs extrêmes.
3- Pourcentages
3A. Proportion dans une population
Soit E une population d’effectif \(n_E\) et soit \(A\) une sous-population de \(E\) d’effectif \(n_A\).
La proportion de la population \(A\) dans \(E\) est :
\(\frac{n_A}{n_E}\)
Exemple :
Dans une population de 600 individus, 72 sont blonds.
La proportion de blonds dans la population est \(\frac{72}{600}=0,12\), soit 12%
Si \(P_A\) est le pourcentage d’une sous-population \(A\) dans une population \(E\) et si \(P_B\) est le pourcentage d’un groupe \(B\) dans la sous-population \(A\), alors le pourcentage du groupe \(B\) dans la population \(E\) est :
\(P_A \times P_B\)
3B. Evolution
Soit une grandeur qui passe d’une valeur initiale \(V_I\) à une valeur finale \(V_F\).
On appelle variation absolue la quantité :
\(V_F – V_I\).
On appelle variation relative la quantité :
\(\frac{V_F-V_I}{V_I}\)
Exemple :
Un prix passe de 40 € à 50 €.
La variation absolue du prix est 50 € – 40 €, soit 10 €.
La variation relative est \(\frac{50-40}{40}=0,25\), soit 25%.
Augmenter une valeur de \(a% \), revient à multiplier cette valeur par \((1+ \frac{a}{100})\).
Diminuer une valeur de \(a% \), revient à multiplier cette valeur par \((1- \frac{a}{100})\).
Soit \(a\) un réel strictement positif.
Le nombre \(t= a – 1\) est le taux d’évolution associé au coefficient multiplicateur \(a\).
\(a=1+t\) est le coefficient multiplicateur associé au taux d’évolution \(t\).
\(t\) et \(t’\) deux taux d’évolutions sont dits taux réciproques si, et seulement si :
\((1+t)(1+t’)=1\).
Exemple :
Une hausse de 25% \((t=+0,25)\) correspond à un coefficient multiplicateur de \((1+\frac{25}{100})=1,25\).
Une baisse de 20% \((t’=-0,20)\) correspond à un coefficient multiplicateur de \((1-\frac{20}{100})=0,8\).
Comme \(1,25 \times 0,8=1\), \(t=0,25\) et \(t’=-0,20\) sont des taux d’évolutions réciproques.