Chapitre 1 : Repérage dans le plan
Chapitre 2 : Milieu et Coordonnées
Chapitre 3 : Distance entre deux Points
1- Repérage dans le plan
- Soit \(O\),\(I\) et \(J\) trois points non alignés d’un plan.
Le triplet ( \(O\),\(I\),\(J\)) constitue un repère du plan.
- Soit ( \(O\),\(I\),\(J\)) un repère du plan.
Le point \(O\) est l’origine du repère.
La droite \((OI)\) est l’axe des abscisses.
La droite \((OJ)\) est l’axe des ordonnées.
- Soit ( \(O\),\(I\),\(J\)) un repère du plan.
Si le triangle \(OIJ\) est rectangle en \(O\), alors le repère est dit orthogonal.
- Soit ( \(O\),\(I\),\(J\)) un repère du plan.
Si le triangle \(OIJ\) est rectangle et isocèle en \(O\) alors le repère est dit orthonormé.
- Soit ( \(O\),\(I\),\(J\)) un repère du plan.
A chaque point \(A\) du plan est associé dans ce repère un couple (\(x\), \(y\)) de réels.
\(x\) et \(y\) sont les coordonnées de \(A\) ; \(x\) est son abscisse et \(y\) est son ordonnée.
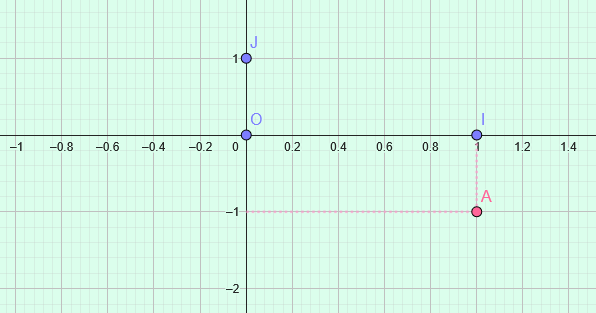
Le repère est orthogonal. L’abscisse du point A est 1 et son ordonnée est -1, on note \(A(1;-1)\)
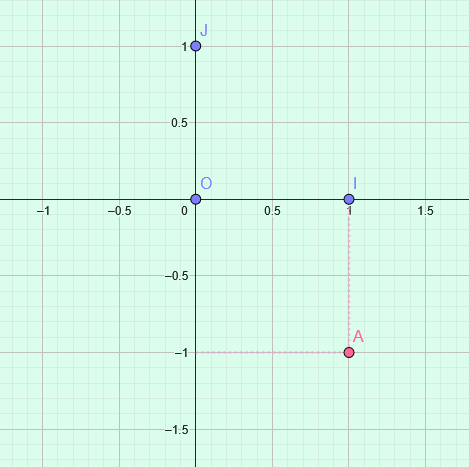
Le repère est orthonormé. L’abscisse du point A est 1 et son ordonnée est -1, on note \(A(1;-1)\)
2- Milieu et coordonnées
Soit \(A(x_a;y_a)\) et \(B(x_b;y_b)\) deux points d’un plan muni d’un repère.
Le mileu \(M\) du sgment \([AB]\) a pour coordonnées \((\frac{x_a+x_b}{2};\frac{y_a+y_b}{2})\)
Remarque : Les coordonnées du milieu d’un segment correspondent à la moyenne arithmétique des coordonnées des extrémités de ce segment.
3- Distance entre deux points
Soit \(A(x_a;y_a)\) et \(B(x_b;y_b)\) deux points d’un plan muni d’un repère orthonormé.
La distance \(AB\) entre les points \(A\) et \(B\) est donnée par : \(AB=\sqrt{(x_b-x_a)^2+(y_b-y_a)^2}\)
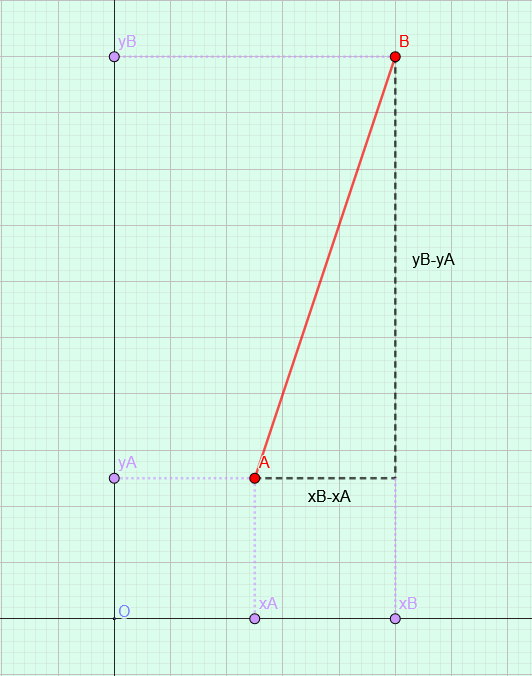
Remarques :
- La formule n’est valable que dans un repère orthonormé.
- Dans la formule ci-dessus, \((x_b-x_a)^2\) peut être remplacé par \((x_a-x_b)^2\) car les nombres \(x_b-x_a\) et \(x_a-x_b\) sont opposés et ont par conséquent le même carré. Il en est de même pour les termes en y.