Chapitre 1 : Notion de fonction
Chapitre 2 : Représentation graphique et variations
1- Notion de fonction
1A. Définition d’une fonction
Une fonction est une relation qui, à un nombre appelé antécédent, associe au plus un autre nombre appelé image.
- On note une fonction en général par une lettre (souvent f, g ou h).
- Si une fonction f associe à un nombre x une valeur unique f(x), on écrit :\(f : x \longmapsto f(x)\)
Exemple : La fonction qui associe à tout nombre x son double est définie par :
\(f(x) = 2x\)
Ainsi, l’image de 3 est \(f(3) = 2 \times 3 = 6\).
1B. Domaine de définition
Le domaine de définition d’une fonction est l’ensemble des nombres pour lesquels elle est définie.
Exemple : La fonction \(f(x) = \frac{1}{x}\) n’est pas définie pour \(x = 0\), car la division par zéro est impossible.
Son domaine de définition est donc \(\mathbb{R} \setminus {0}\).
1C. Image d’une fonction
L’image d’une fonction est l’ensemble des valeurs prises par \(f(x)\) lorsque \(x\) parcourt son domaine de définition.
Exemple : Pour la fonction \(f(x) = x^2\), l’image de f est \(\mathbb{R}^{+}\) (ensemble des réels positifs ou nuls), car \(x^2\) est toujours positif ou nul.
2- Représentation graphique et variations
2A. Représentation graphique
La représentation graphique d’une fonction f est l’ensemble des points de coordonnées \((x, f(x))\) dans un repère.
Propriétés :
- Si une fonction est définie sur un intervalle, sa courbe ne doit jamais être coupée verticalement plus d’une fois en un même point.
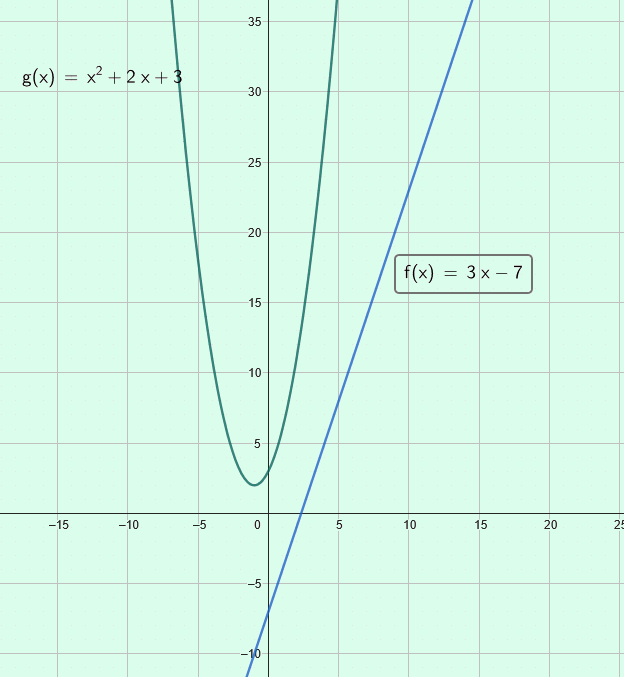
- Une fonction linéaire \(f(x) = ax\) ou affine \(f(x) = ax + b\) a pour représentation graphique une droite.
- Une fonction quadratique \(g(x) = ax^2 + bx + c\) est représentée par une parabole.
2B. Sens de variation et extrema
Une fonction peut être croissante, décroissante ou constante sur un intervalle donné.
- Croissante : Si pour tout \(x_1 < x_2\), on a \(f(x_1) \leq f(x_2)\).
- Décroissante : Si pour tout \(x_1 < x_2\), on a \(f(x_1) \geq f(x_2)\).
- Constante : Si \(f(x_1) = f(x_2)\) pour tout \(x_1, x_2\).
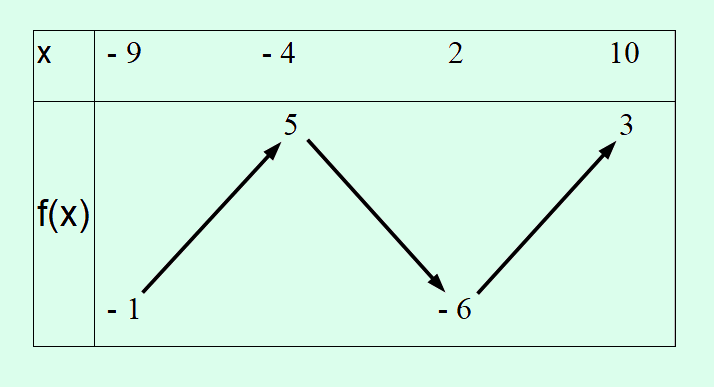
Dans ce cas, la fonction admet un minimum global en \(x = 2\) avec \(f(2) = -6\).
Un extremum d’une fonction est une valeur où elle atteint un maximum ou un minimum local.
- Un minimum local en \(x_0\) signifie que \(f(x_0) \leq f(x)\) pour \(x\) proche de \(x_0\).
- Un maximum local en \(x_0\) signifie que \(f(x_0) \geq f(x)\) pour \(x\) proche de \(x_0\).
Ces extrema peuvent être identifiés à partir du tableau de variation.rmations dans un tableau de variation. Les points hauts et bas d’une courbe sont appelés extrema (maximums et minimums).