1- Inégalités
1A. Règles de calcul sur les inégalités
\(a\),\(b\),\(c\) et \(d\) désignent quatre réels.
On peut ajouter ou soustraire le même nombre aux deux membres d’une inégalité :
\(a<b⇔a+c<b+c\) et \(a<b⇔a-c<b-c\).
On peut multiplier ou diviser par un même nombre strictement positif les deux membres d’une inégalité :
Si \(c>0\) alors \(a<b⇔ac<bc\) et \(a<b⇔\frac{a}{c}<\frac{b}{c}\) .
On peut multiplier ou diviser par un même nombre strictement négatif les deux membres d’une inégalité en changeant le sens de l’inégalité :
Si \(c<0\) alors \(a<b⇔ac>bc\) et \(a<b⇔\frac{a}{c}>\frac{b}{c}\) .
On peut ajouter membre à membre deux inégalités de même sens :
Si \(a<b\) et \(c<d\) alors \(a+c<b+d\)
Remarques :
- La réciproque de cette propriété est fausse.
- On ne peut pas soustraire membre à membre deux inégalités de même sens.
1B. Encadrements
\(a\),\(b\) et \(c\) désignent trois réels.
- Le système \(\left\{\begin{array}{6}a<b\\b<c\end{array}\right.\) s’écrit aussi \(a<b<c\) : on dit que l’on a une double inégalité ou un encadrement de \(b\).
- Dans un encadrement \(a<b<c\), \(c-a\) est l’amplitude de l’encadrement.
- Sur les encadrements, on peut appliquer les mêmes règles de calcul que sur les inégalités.
2- Intervalles
2A. Notion d’intervalle
Un intervalle est l’ensemble des abscisses d’une partie » en un seul morceau » d’une droite graduée.
Soit \(a\) et \(b\) deux réels avec \(a<b\).
intervalles bornés :

intervalles non bornés :

2B. Intersection et réunion
Soit \(A\) et \(B\) deux Ensembles.
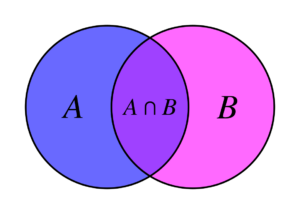
L’intersection de \(A\) et \(B\), notée \(A∩B\), est l’ensemble des éléments appartenant à la fois à \(A\) et à \(B\).
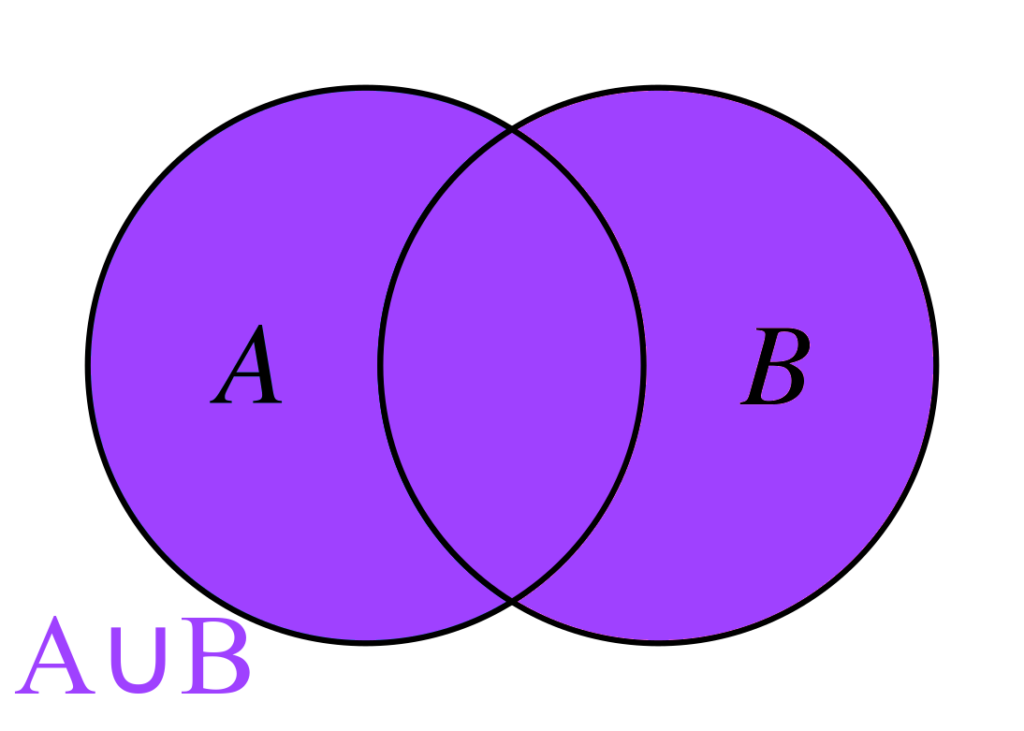
La réunion (ou union ) de \(A\) et \(B\), notée \(A∪B\), est l’ensemble des éléments appartenant à \(A\) ou à \(B\).
3- Inéquations du premier degré
3A. Définition
Une inéquation du premier degré est une inégalité faisant intervenir une variable sous forme affine (c’est-à-dire sans exposant supérieur à 1). Elle peut s’écrire sous la forme :
\(ax + b < 0, \quad ax + b \leq 0, \quad ax + b > 0, \quad ax + b \geq 0\)
avec \(a\) et \(b\) des réels donnés et \(a \neq 0\).
3B. Résolution d’une inéquation du premier degré
- Isoler le terme en \(x\) : On soustrait ou ajoute le terme constant des deux côtés de l’inégalité :\(ax + b < 0 \quad \Rightarrow \quad ax < -b\)
- Diviser par \(a\) :
- Si \(a > 0\), on divise sans changer le sens de l’inégalité :\(x < \frac{-b}{a}\)
- Si \(a < 0\), on divise et on change le sens de l’inégalité :\(x > \frac{-b}{a}\)
Exemple de résolution
Résolvons l’inéquation suivante :
\(2x – 5 \geq 3\)
- Ajouter 5 aux deux membres :\(2x \geq 8\)
- Diviser par 2 :\(x \geq 4\)
La solution est \([4; +\infty[\).
Les inéquations du premier degré se résolvent comme des équations, en prenant garde à inverser le sens de l’inégalité si on divise par un nombre négatif. Leur solution peut être représentée sur une droite graduée ou sous forme d’intervalle.