Chapitre 2 : Fonction racine carrée
1- Fonction carrée
1A. Définition
- La fonction carré est la fonction f définie sur \(\mathbb{R}\) qui, à tout réel \(x\), associe son carré \(x^2\) :
On note \(f(x)=x^2\) ou \(f:x \longmapsto x^2\)
1B. Variations de la fonction carré
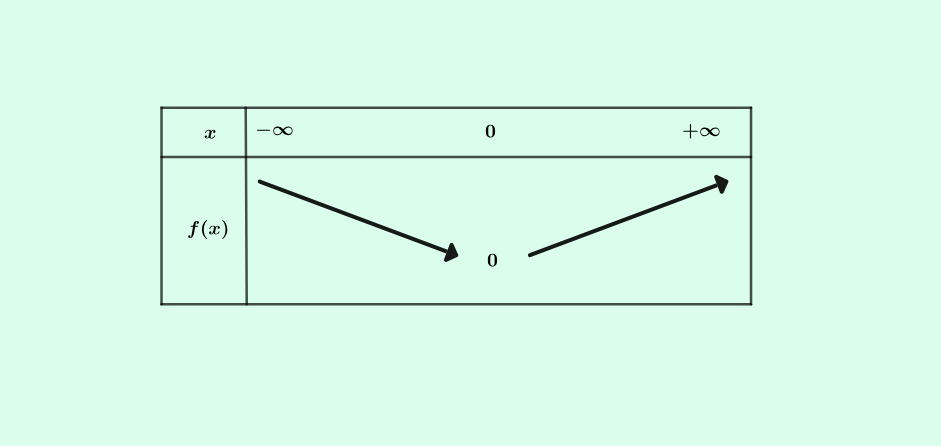
- La Fonction carré est décroissante sur \(]-\infty\ ;\ 0\ ]\) et croissante sur \([\ 0\ ; +\infty[\)
Son tableau de variations est :
1C. Représentation graphique
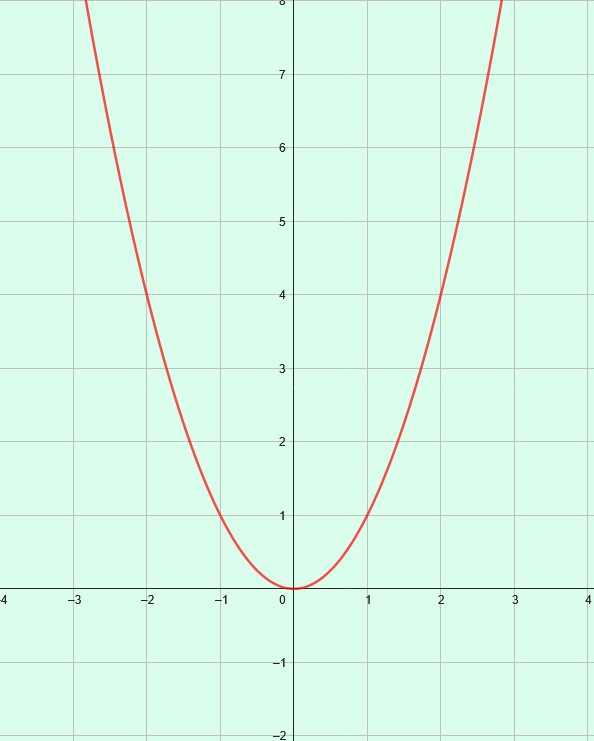
La représentation graphique de la fonction carré est une parabole.
- Pour tout réel \(x\), \(x^2\) est un nombre positif.
- Dans un repère orthogonal, la parabole représentant la fonction carré est symétrique par rapport à l’axe des ordonnées.
- Deux nombres opposés ont le même carré.
2- Fonction racine carrée
2A. Définition
On appelle fonction racine carrée la fonction qui, à tout réel positif, associe sa racine carrée.
La fonction racine carrée est définie sur \(\mathbb{R}^{+}=[\ 0\ ;+\infty[\) par \(f(x)=\sqrt{x}\)
2B. Variations de la fonction racine carrée
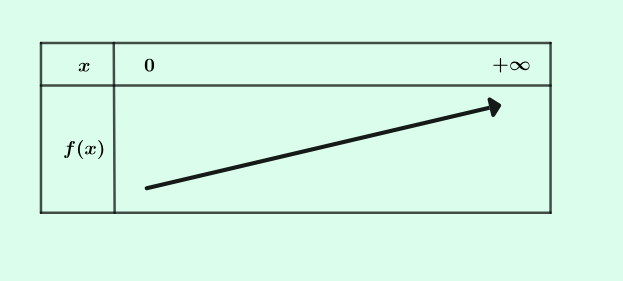
La fonction racine carrée est croissante sur \([\ 0\ ;+\infty[\).
Son tableau de variation est :
2C. Représentation graphique
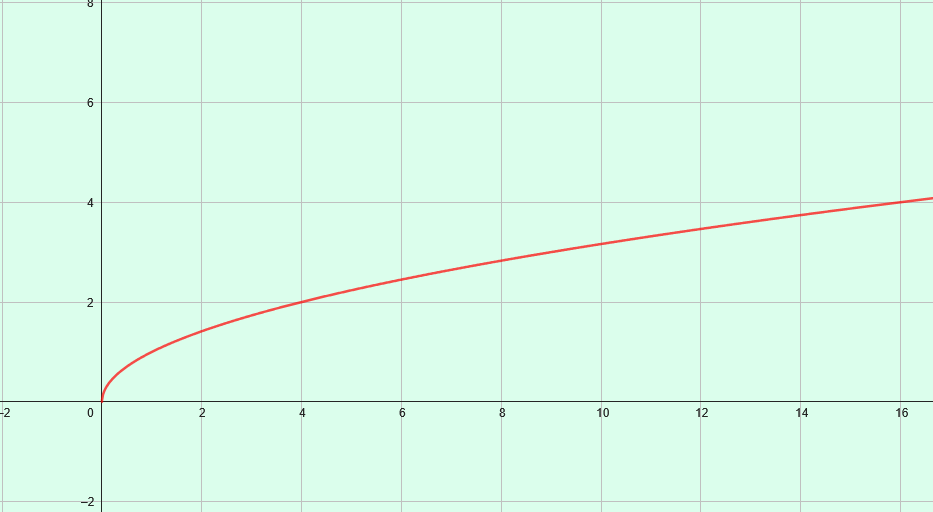
Remarque : La représentation graphique de la fonction racine carrée est une demi-parabole.
3- Fonction cube
3A. Définition
- On appelle fonction cube la fonction qui, à tout réel, associe son cube.
- La fonction cube est définie sur \(\mathbb{R}\) par \(f(x)=x^3\).
3B. Variations de la fonction cube
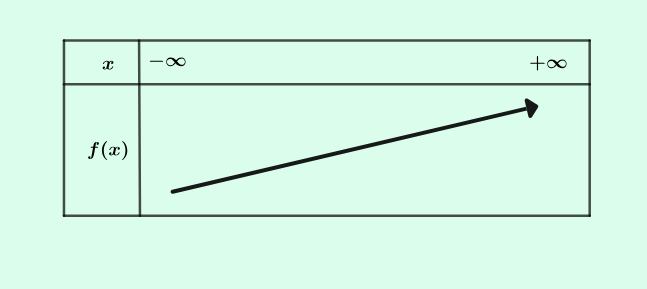
La fonction cube est croissante sur \(\mathbb{R}\)
Son tableau de variation est :
3C. Représentation graphique
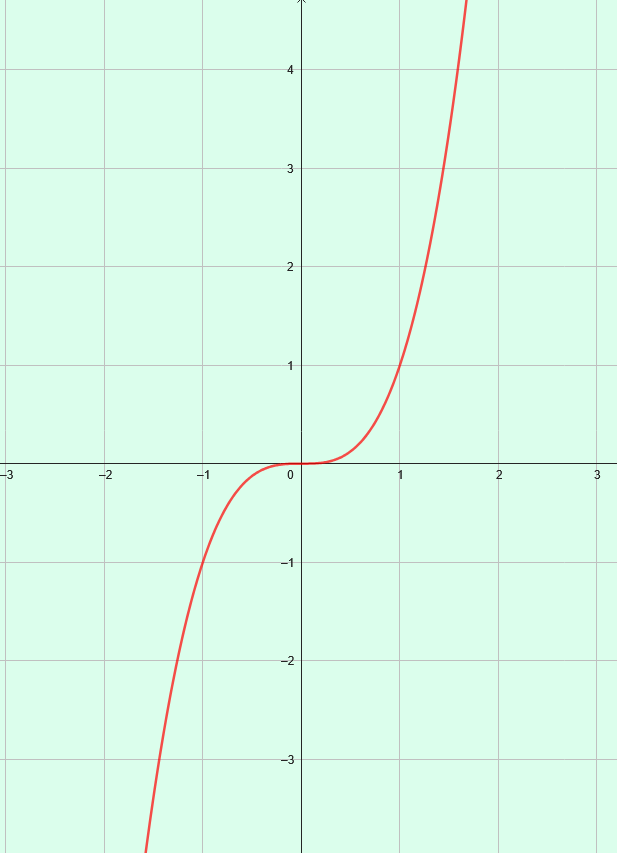
Remarque : La représentation graphique de la fonction cube est symétrique par rapport à l’origine du repère.
4- Fonction inverse
4A. Définition
- On appelle fonction inverse la fonction qui, à tout réel non nul, associe son inverse.
- La fonction inverse est définie sur \(\mathbb{R}_*\) par \(f(x)=\frac{1}{x}\).
Remarques :
- Pour tout réel \(x\) non nul, \(x \times \frac {1}{x}=1\).
- \(0\) n’a pas d’inverse car pour tout réel \(x\),\(0 \times x=0\).
4B. Variations de la fonction inverse
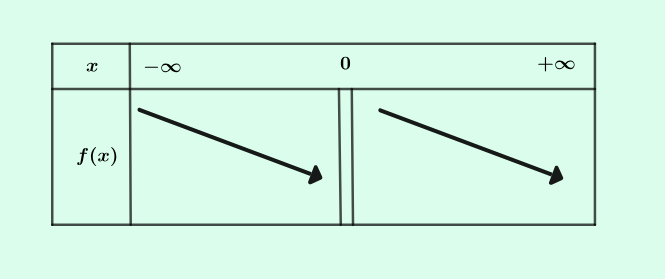
La fonction inverse est décroissante sur \(]-\infty\ ;\ 0\ [\), ainsi que sur \(]\ 0\ ;+\infty[\)
La fonction inverse a le tableau de variations ci dessous
La double barre au-dessous de 0 indique que la fonction inverse n’est pas définie en \(0\).
4C. Représentation graphique
- On appelle hyperbole la représentation graphique de la fonction inverse
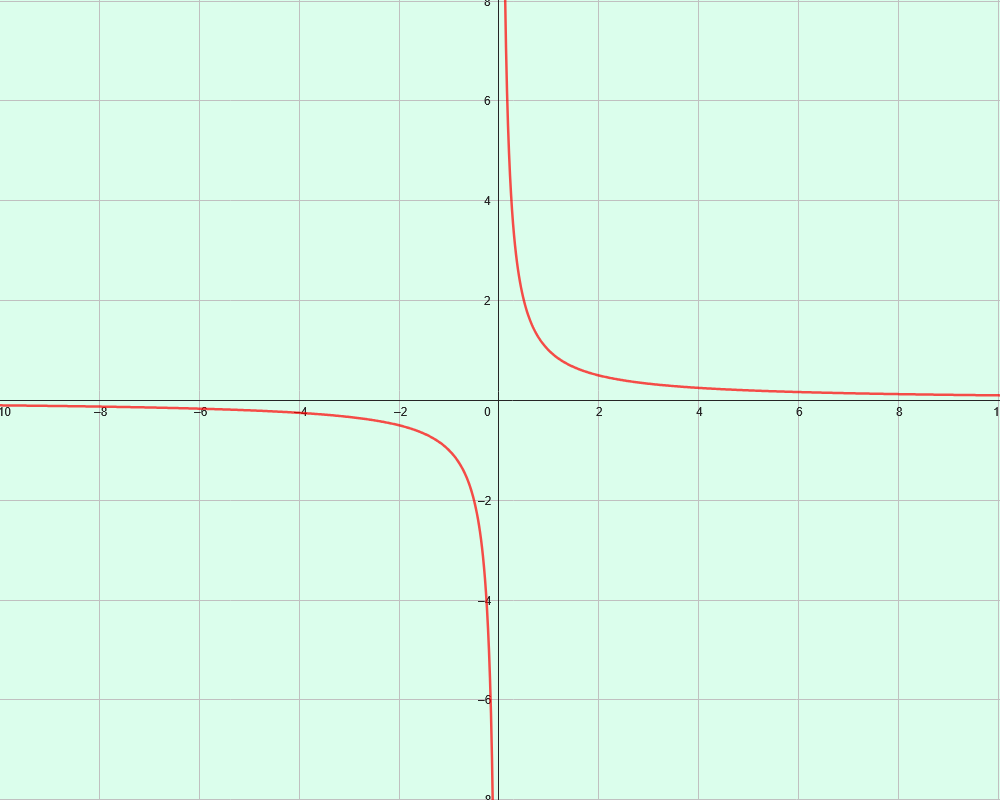
Remarques :
- Cette hyperbole a pour équation \(y=\frac{1}{x}\).
- L’hyperbole admet un centre de symétrie qui est ici l’origine du repère.