Les exercices sont ici : Exercices Calcul Littéral – Ensemble de nombres
Chapitre 1 : Ensemble de nombres
1- Ensemble de nombres
1A. Définitions
ℕ désigne l’ensemble des entiers naturels ( entiers positifs ou nuls ). ℕ = { 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; … }
ℤ désigne l’ensemble des entiers relatifs ( entiers positifs, nuls ou négatifs ). ℤ = { … ; -4 ; -3 ; -2 ; -1 ; 0 ; 1 ; 2 ; 3 ; 4 ; … }
𝔻 désigne l’ensemble des nombres décimaux ( nombres qui peuvent s’écrire sous la forme \(\frac{a}{10^n}\) avec a un entier relatif et n un entier naturel ) Autrement dit, c’est un nombre à virgule qui possède un nombre fini de chiffres après la virgule.
Exemple : 2,2518 est un nombre décimal ( il peut s’écrire \(\frac{22518}{10^4}\) mais 1,33333333…… ne l’est pas. )
ℚ désigne l’ensemble des nombres rationnels ( tout nombre que l’on peut écrire sous la forme \(\frac{a}{b}\) avec a et b deux entiers relatifs \(\quad b \neq 0\) )
ℝ désigne l’ensemble des nombres réels, tous les nombres connus au niveau 2nd sont des nombres réels.
1B. Inclusion
Tout entier naturel est également un entier relatif : on dit alors que ℕ est inclus dans ℤ et on note ℕ ⊂ ℤ. Le symbole ⊂ se lit » inclus dans « .
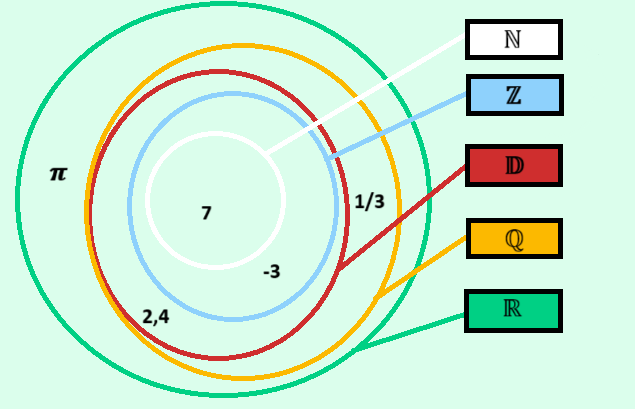
On a ℕ ⊂ ℤ ⊂ 𝔻 ⊂ ℚ ⊂ ℝ
1C. Notations
On peut faire suivre le nom d’un ensemble de nombres du symbole * pour désigner l’ensemble de ses nombres autres que le nombre 0. Ainsi ℕ* désigne l’ensemble des entiers naturels non nuls. ℕ*={ 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; … }
On peut faire suivre le nom d’un ensemble de nombres du symbole + ( respectivement – ) pour désigner l’ensemble de ses nombres positifs ( respectivement négatif ). Ainsi ℝ– désigne l’ensemble des réels négatifs ou nuls.
Remarque : On a donc ℤ+ = ℕ
2- Calcul littéral
2A. Développement
Développer, c’est transformer un produit ( x ) en une somme algébrique ( + )
Règles de distributivité :
\(a(b + c) = ab + ac\)
\(a(b-c) = ab-ac\)
\((a + b)(c + d) = ac + ad + bc + bd\)
Identités remarquables :
\((a+b)^2=a^2+2ab+b^2\)
\((a-b)^2=a^2-2ab+b^2\)
\((a+b)(a-b)=a^2-b^2\)
Comment utiliser les identités remarquables ?
2B. Factorisation
Factoriser, c’est transformer une somme algébrique ( + ) en un produit ( x )
Règles de distributivité :
\(ab+ac=a(b+c)\)
\(ab-ac=a(b-c)\)
Identités remarquables :
\(a^2+2ab+b^2=(a+b)^2\)
\(a^2-2ab+b^2=(a-b)^2\)
\(a^2-b^2=(a-b)(a+b)\)
Comment utiliser les identités remarquables ?
3- Equations
3A. Définitions
Une égalité comportant un nombre inconnu s’appelle une équation.
Résoudre une équation, c’est déterminer les valeurs de l’inconnue qui rendent vraie l’égalité. On dit que ces valeurs sont les solutions de l’équation.
Deux équations ayant les mêmes solutions sont dites équivalentes. Entre deux équations équivalentes, on utilise le symbôle ⇔.
3B. Méthodes de résolutions
Comment résoudre une équation du premier degrés ?
On peut ajouter ou soustraire le même nombre aux deux membres d’une équation pour obtenir une équation équivalente.
On peut multiplier ou diviser par le même nombre non nul les deux membres d’une équation pour obtenir une équation équivalente.
Equation produit-nul :
Un produit de facteurs est nul, si, et seulement si, l’un au moins de ses facteurs est nul. Ceci s’écrit en symboles mathématiques :
\(A×B=0 ⇔ A=0\) ou \(B=0\)
Equation \(x^2=a\) avec \(a>0\) :
Pour \(a>0\), \(x^2=a ⇔ x=\sqrt{a}\) ou \(x=-\sqrt{a}\)
L’équation \(x^2=a\), avec \(a<0\) n’a pas de solution.
Produit en croix :
Soit a,b,c et d quatre nombres.
\(\frac{a}{b} = \frac{c}{d}⇔ ad = bc\) , \(\quad b \neq 0\) et\(\quad d \neq 0\)