Test de sommaire ( va être modifié )
Sommaire
1- Triangles rectangles
1A. Définition
- Théorème de Pythagore
Si un triangle est rectangle, alors le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés.
Fiche technique
- Réciproque du théorème de Pythagore
Si dans un triangle le carré d’un côté est égal à la somme des carrés des deux autres côtés, alors ce triangle est rectangle au sommet opposé au plus grand côté.
Fiche technique
- Centre du cercle circonscrit à un triangle rectangle
Si un triangle est rectangle, alors le centre de son cercle circonscrit est le milieu de son hypoténuse.
- Triangle inscrit dans un demi-cercle
Si un côté d’un triangle est un diamètre de son cercle circonscrit, alors ce triangle est rectangle au somment opposé au côté diamètre.
- Triangle rectangle et angles
Si un triangle est rectangle, alors ses angles aigus sont complémentaires.
Si un triangle possède deux angles complémentaires, alors ce triangle est rectangle.
- Trigonométrie
Soit un triangle \(ABC\) rectangle en \(A\) :
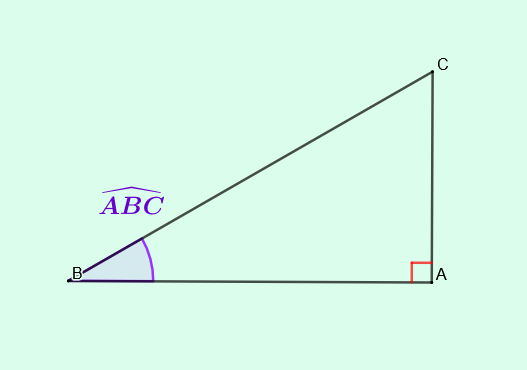
\(cos(\widehat{ABC})=\frac{\text{côté adjacent à }\widehat{B}}{\text{hypoténuse }}=\frac{AB}{BC}\)
\(sin(\widehat{ABC})=\frac{\text{côté opposé à }\widehat{B}}{\text{hypoténuse }}=\frac{AC}{BC}\)
\(tan(\widehat{ABC})=\frac{\text{côté opposé à }\widehat{B}}{\text{côté adjacent à }\widehat{B}}=\frac{AB}{BC}\)
Moyen Memnotechnique : SOHCAHTOA sinus opposé/hypo, cosinus adjacent/hypo, tangeante opposé/adjacent
Pour tout angle aigu \(\widehat{a}\) d’un triangle rectangle, on a :
\(cos^2(\widehat{a})+sin^2(\widehat{a})=1\)
2- Droites
- Projeté orthogonal
Le projeté orthogonal d’un point \(C\) sur une droite \((AB)\) est le point \(H\) intersection de la droite perpendiculaire à \((AB)\) passant par \(C\).
Si \(H\) est le projeté orthogonal d’un point \(C\) sur une droite \((AB)\), alors \(H\) est le point de \((AB)\) le plus proche de \(C\).
- Hauteurs d’un triangle
Une hauteur d’un triangle est une droite passant par un sommet et perpendiculaire au côté opposé.
Dans un triangle, les hauteurs sont concourantes en un point appelé orthocentre du triangle.
Dans un triangle \(ABC\), le pied de la hauteur issue de \(C\) est \(H\) le projeté orthogonal de \(C\) sur \((AB)\).
- Médiatrices d’un triangle
Une médiatrice d’un triangle est une droite passant par le milieu d’un côté et perpendiculaire à ce côté.
Dans un triangle, les médiatrices sont concourantes en un point appelé centre du cercle circonscrit.
Dans un triangle \(ABC\), le milieu d’un côté est \(H\) le projeté orthogonal du centre du cercle circonscrit sur ce côté.
3- Aires
En cours de création
4-Volumes
En cours de création